| Wichtige Defintionen: Grenzwert einer Zahlenfolge |
Eine Zahlenfolge (ak) hat den Grenzwert g =Df.
Für jedes e > 0 gilt für fast alle k aus N:
ak liegt innerhalb der e-Umgebung von g.
Als e-Umgebung versteht man das Intervall (g-e < g < g+e). |
| Oder: |
Eine Zahlenfolge (ak) hat den Grenzwert g =Df.
Für jedes e > 0 gilt für fast alle k aus N:
|ak - g| < e. |
| Übung: Wie viele Zahlenfolgenglieder liegen außerhalb der e-Umgebung von g?. |
(ak)=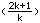
mit g=2 und e=0,01 folgt: |
Ansatz:
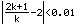 |
Lösung der Ungleichung:
k >
Außerhalb liegen also:
Zahlenfolgenglieder. |
Die Antwort ist |
(ak)=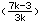
mit g=7/3 und einer 0,05-Umgebung folgt: |
Ansatz:
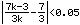 |
Lösung der Ungleichung:
k >
Außerhalb liegen also:
Zahlenfolgenglieder. |
Die Antwort ist |
(ak)=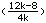
mit g=3 und einer
-Umgebung folgt: |
Ansatz:
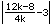 <
< |
Lösung der Ungleichung (max. auf 2 Stellen nach Komma genau):
k >
Außerhalb liegen also:
Zahlenfolgenglieder. |
Die Antwort ist |
| Wichtige Defintionen: |
Eine Zahlenfolge, die einen Grenzwert hat, heißt konvergent.
Folgen, die keinen Grenzwert haben, heißen divergent.
Hat eine Folge den Grenzwert 0, dann heißt sie auch Nullfolge (NF).
Konstante Folgen (ak) = (c) haben den Grenzwert c.
Ist eine Folge konvergent, dann hat sie genau einen Grenzwert.
Man schreibt dafür auch kurz:
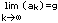 |
| Wichtiger Satz: Grenzwertsatz für Zahlenfolgen |
| Wenn die Folgen (ak) und (bk) konvergieren, so konvergieren
auch die Folgen (ak + bk), (ak - bk)
(ak * bk) und (ak / bk), falls (bk))
keine Nullfolge ist. |
| Übung: Für die folgenden Folgen sollen Grenzwerte mit Hilfe des Grenzwertsatzes
berechnet werden. |
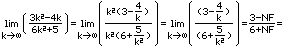
|
Die Antwort ist |
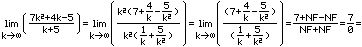
|
Die Antwort ist |
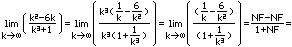
|
Die Antwort ist |
| Merke: Ergänze die drei Merksätze! |
| 1. Sind die
Potenzen von k im Zähler und Nenner gleich, dann ist der Grenzwert der Folge
gleich dem
aus den
vor den
Potenzen. |
Die Antwort ist |
| 2. Befindet sich die
Potenz von k im Zähler, dann ist die Folge divergent.
|
Die Antwort ist |
| 3. Befindet sich die höchste Potenz von k im
, dann handelt es sich um eine Nullfolge (NF).
|
Die Antwort ist |