Merke: Grenzwertberechnungen sind ein wichtiges Hilfsmittel z.B. zur
Problemlösung in der Differential- und Integralrechnung. So ist der Differentialquotient
einer Funktion f an der Stelle x0 der Grenzwert des Differenzenquotienten. Und das
bestimmte Integral ist der Grenzwert einer Partialsummenfolge von
Flächenelementen im Intervall I[a,b] unterhalb einer Funktion f im 1. Quadranten.
Des weiteren untersucht die Schulmathematik mit Hilfe von Grenzwerten das Verhalten von
Funktionen im Unendlichen, ermittelt Asymptotengleichungen und Polstellenumgebungen und löst
Unendlichkeitsphänomene (siehe Beispiele unten). |
| Übungen: Unendlichkeitsphänomene |
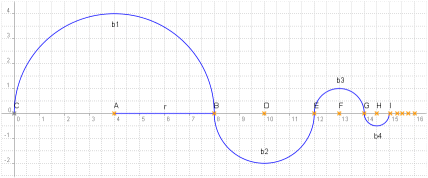Beispiel A) Das Bild zeigt eine Schlange in Form aneinander gelegter Halbkreise. Der erste Halbkreis
mit der Bogenlänge b1 hat den Radius r. Der Radius jedes weiteren Halbkreises ist halb so groß
wie der Radius seines unmittelbaren Vorgängers. (Quelle: LB Ma 11, VuW 1981, S. 123 ff)
|
| 1) Die Längen b1, b2, b3,...,bn,... der Halbkreisbögen
bilden eine unendliche geometrische Folge (bn). Es gilt: b1 = πr. Geben Sie eine explizite
Zuordnungsvorschrift dieser Folge in Abhängigkeit von r an. |
| a) |
b) |
c) |
d) |
| (bn) = (2π r n) |
(bn) = (π r /2(n-1)) |
(bn) = (π r /2n) |
(bn) = (π r /2) |
| 2) Die Summe sn der ersten n Glieder der Folge (bn) kann mit Hilfe
der allgemeinen Summenformel für geometrische Zahlenfolgen sn = b1 (qn-1) / (q-1)
berechnet werden. Wie lautet die konkrete Summenformel für die Summe der Halbkreise? (Hinweis:
q ist der Quotient der geometrischen Folge (bn)). |
| a) |
b) |
c) |
d) |
| (sn) = (2πr(1-1/2n)) |
(sn) = (π r /(n-1)) |
(sn) = (π r 2n) |
(sn) = (2π r) |
| 3) Der Grenzwert der Summe sn für n → ∞ beschreibt die Länge L der unendlich
langen Schlange. Wie lang ist die Schlange, wenn für den Radius die Länge r=1 angenommen wird?
(Hinweis: Berechne lim(sn) für n → ∞) |
| b) |
c) |
d) |
a) |
| L = lim(sn) = π |
L = lim(sn) = 6 |
L = lim(sn) = ∞ lang |
L = lim(sn) = 2π |
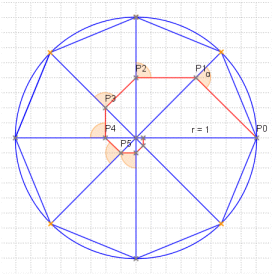Beispiel B) Gegeben sei ein regelmäßiges in den Einheitskreis einbeschriebenes Achteck.
Man fälle von einer Ecke P0 das Lot auf den Radius, der zu einer benachbarten Ecke des Achtecks
gezogen ist. Der Lotfußpunkt sei P1. Von diesem fälle man wiederum das Lot auf den Radius, der zur
nächsten Ecke des Achtecks führt usw. Wir erhalten eine Schnecke, die aus aneinander gereihten Loten
besteht (siehe Bild). (Quelle: LB Ma 11, VuW 1981, S. 123 ff)
|
| 1) Die Längen p1=P0P1, p2=P1P2, p3=P2P3,...,pn=P(n-1)Pn,... der Lote
bilden eine unendliche geometrische Folge (pn). Es gilt: p1 = √(0.5).
Ermitteln Sie p2 und p3. Wie lautet die explizite Zuordnungsvorschrift dieser Folge (pn)? |
| a) |
b) |
 |
 |
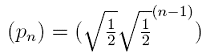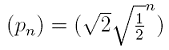| c) |
d) |
 |
 |
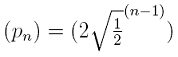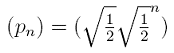| 2) Die Summe sn der ersten n Glieder der Folge (pn) kann mit Hilfe
der allgemeinen Summenformel für geometrische Zahlenfolgen sn = p1 (qn-1) / (q-1)
berechnet werden. Wie lautet die konkrete Summenformel für die Summe der Lote? (Hinweis:
q ist der Quotient der geometrischen Folge (pn)). |
| a) |
b) |
 |
 |
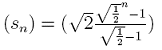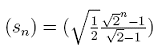| c) |
d) |
 |
 |
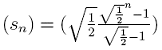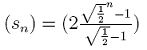| 3) Der Grenzwert der Summe sn für n → ∞ beschreibt die Länge L der unendlich
langen Schnecke. Wie lang ist die Schnecke?
(Hinweis: Berechne lim(sn) für n → ∞) |
| a) |
b) |
c) |
d) |
| L = lim(sn) = π |
L = lim(sn) = √(0.5)+1 |
L = lim(sn) = ∞ lang |
L = lim(sn) = 2π |
